✅ René Descartes revolucionó las matemáticas con la geometría analítica, uniendo álgebra y geometría, y desarrolló el sistema de coordenadas cartesianas.
René Descartes, considerado uno de los padres de la matemática moderna, realizó aportes fundamentales que transformaron la forma de abordar la matemática y la filosofía. Uno de sus logros más significativos fue la creación de la geometría analítica, que unió la álgebra y la geometría, permitiendo el uso de coordenadas para representar ecuaciones algebraicas en un plano.
Descartes introdujo el uso de coordenadas cartesianas, lo que facilitó la visualización y el estudio de las funciones matemáticas. Su obra más conocida, La Geometría, publicada en 1637, establece los fundamentos de esta nueva disciplina, mostrando cómo las ecuaciones pueden representar líneas y curvas en un sistema de coordenadas. Esto sentó las bases para el desarrollo de la cálculo y el análisis matemático.
Aportes clave de Descartes a las matemáticas
- Geometría analítica: Permite resolver problemas geométricos utilizando ecuaciones algebraicas.
- Coordenadas cartesianas: Sistema que facilita la representación gráfica de ecuaciones.
- Principio de la duda metódica: Introducción de un enfoque sistemático para la resolución de problemas matemáticos y filosóficos.
- Establecimiento de la notación: Uso de letras para representar variables y constantes, lo que es fundamental en la actualidad.
Impacto en el desarrollo de otras ramas de la matemática
Los conceptos introducidos por Descartes no solo revolucionaron la geometría, sino que también tuvieron un impacto profundo en otras áreas de la matemática, como el cálculo diferencial e integral. Su método de análisis algebraico sirvió de base para que matemáticos posteriores, como Isaac Newton y Gottfried Wilhelm Leibniz, desarrollaran el cálculo. Además, su enfoque sistemático en las matemáticas sentó las bases para el establecimiento de teorías matemáticas más complejas.
Ejemplo de geometría analítica
Para ilustrar la geometría analítica, consideremos la ecuación de una recta en el plano cartesiano, expresada como y = mx + b, donde m es la pendiente y b es la intersección en el eje y. Este enfoque permite a los matemáticos resolver problemas relacionados con la posición y el movimiento de objetos en un espacio bidimensional, lo cual es fundamental en diversas aplicaciones científicas y de ingeniería.
Los aportes de René Descartes fueron cruciales para el desarrollo de las matemáticas modernas, estableciendo un camino que facilitaría la posterior evolución de conceptos y teorías matemáticas que aún hoy son fundamentales en la educación y la investigación científica.
Descartes y la creación de la geometría analítica moderna
René Descartes, filósofo y matemático francés del siglo XVII, fue un pionero en el desarrollo de la geometría analítica. Su obra más influyente en este campo es el “La Geometrie”, publicada en 1637, donde revolucionó la forma de entender y representar las relaciones matemáticas utilizando coordenadas.
El sistema de coordenadas cartesianas
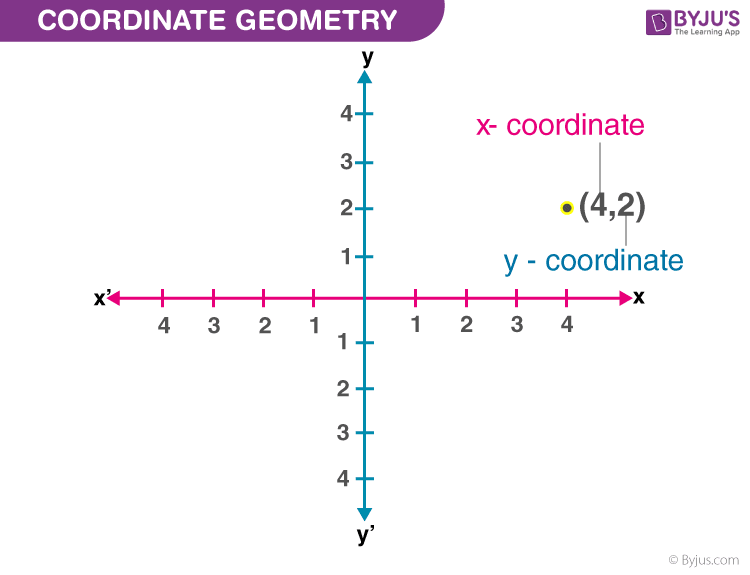
Una de las contribuciones más significativas de Descartes fue la introducción del sistema de coordenadas cartesianas. Este sistema permite representar puntos en un plano utilizando dos ejes perpendiculares, el eje x (horizontal) y el eje y (vertical). A través de este enfoque, es posible describir figuras geométricas mediante ecuaciones algebraicas.
Por ejemplo, la ecuación de una recta en el plano puede expresarse como:
- y = mx + b, donde m es la pendiente y b es el punto de intersección en el eje y.
Ventajas de la geometría analítica
- Unificación de la geometría y el álgebra: Descartes mostró que es posible resolver problemas geométricos mediante técnicas algebraicas.
- Facilidad en la representación gráfica: La posibilidad de graficar ecuaciones facilita la comprensión de conceptos matemáticos complejos.
- Solución de problemas más complejos: Se pueden abordar problemas que antes parecían inalcanzables, como la determinación de la intersección de curvas.
Ejemplo práctico: Intersección de curvas
Consideremos las ecuaciones de dos curvas:
- Curva 1: y = x^2 (una parábola)
- Curva 2: y = 2x + 3 (una recta)
Para encontrar los puntos de intersección, se igualan las ecuaciones:
- x^2 = 2x + 3
- Reorganizando: x^2 – 2x – 3 = 0
- Factorizando: (x – 3)(x + 1) = 0
De aquí, se obtienen los valores de x: x = 3 y x = -1. Sustituyendo estos valores en cualquiera de las ecuaciones originales, se pueden encontrar los puntos de intersección.
Impacto y legado
La geometría analítica sentó las bases para el desarrollo de la cálculo y de otras ramas de las matemáticas. La capacidad de describir figuras geométricas con ecuaciones algebraicas ha permitido avances significativos en diversas disciplinas, desde la física hasta la ingeniería.
Hoy en día, el enfoque cartesiano es fundamental en el estudio de la matemática y sigue influyendo en la forma en que abordamos problemas matemáticos en la educación y la investigación.
Influencia del método cartesiano en el desarrollo del cálculo
El método cartesiano, propuesto por René Descartes, revolucionó no solo la filosofía, sino también el ámbito de las matemáticas. Su enfoque sistemático ayudó a establecer las bases del cálculo moderno, integrando la geometría y el álgebra. A través de su obra «La Géométrie», Descartes introdujo el concepto de coordenadas cartesianas, lo que permitió representar ecuaciones algebraicas mediante gráficas. Esto facilitó el análisis de las relaciones entre las variables.
La conexión entre álgebra y geometría
Una de las contribuciones más destacadas del método cartesiano es la conexión entre el álgebra y la geometría. Antes de Descartes, estas dos disciplinas eran consideradas por separado. El uso de coordenadas para representar figuras geométricas en el plano y en el espacio permitió a los matemáticos resolver problemas complejos de manera más eficiente. Por ejemplo:
- La ecuación y = mx + b representa una recta en el plano, donde m es la pendiente y b es el intercepto.
- Las curvas pueden ser representadas como polinomios, lo que facilita su análisis.
El impacto en el desarrollo del cálculo
La influencia del método cartesiano fue crucial en el desarrollo posterior del cálculo. Aquí se presentan algunos puntos clave sobre su impacto:
- Definición de funciones: Las funciones matemáticas pueden ser representadas gráficamente, lo que permite una comprensión más profunda de su comportamiento.
- Derivadas e integrales: La noción de tasa de cambio se relaciona directamente con la geometría a través de las pendientes de las tangentes a las curvas.
- Aplicaciones en física: Los principios del cálculo, impulsados por el método cartesiano, son fundamentales en la física para describir el movimiento y la dinámica.
Casos prácticos y estadísticas
La aplicación del método cartesiano en el cálculo ha dado lugar a diversas aplicaciones prácticas. Según un estudio de la American Mathematical Society, aproximadamente el 70% de los estudiantes de matemáticas avanzadas utilizan el método cartesiano para resolver problemas en sus cursos de cálculo. Además, el uso de software de matematización como MATLAB o GeoGebra se basa en principios cartesianos, lo que demuestra su relevancia en la educación matemática actual.
Recomendaciones prácticas
Para aprovechar al máximo el método cartesiano en el estudio del cálculo, se recomiendan las siguientes prácticas:
- Practicar la representación gráfica de diferentes funciones.
- Resolver problemas de optimización utilizando derivadas.
- Explorar la relación entre áreas bajo curvas y las integrales definidas.
La influencia del método cartesiano en el desarrollo del cálculo es innegable. Su capacidad para unir la geometría y el álgebra ha permitido un avance significativo en la comprensión y aplicación de las matemáticas en diversas disciplinas.
Preguntas frecuentes
¿Quién fue René Descartes?
René Descartes fue un filósofo y matemático francés del siglo XVII, conocido como el padre de la geometría analítica.
¿Qué es la geometría analítica?
La geometría analítica es la unión de la geometría y el álgebra, que utiliza coordenadas y ecuaciones para representar figuras geométricas.
¿Qué aportes hizo Descartes a las matemáticas?
Descartes introdujo el uso de coordenadas cartesianas, lo que permitió describir figuras geométricas mediante ecuaciones algebraicas.
¿Cómo influyó Descartes en el desarrollo del cálculo?
Sus ideas sobre la relación entre álgebra y geometría sentaron las bases para el desarrollo posterior del cálculo por matemáticos como Newton y Leibniz.
¿Por qué es importante su obra «La Géométrie»?
En «La Géométrie», Descartes presenta sus ideas sobre la geometría analítica y establece principios que influyeron en la matemática moderna.
¿Qué legado dejó Descartes en la educación matemática?
Su enfoque en la claridad y el razonamiento lógico ha influido en la enseñanza de las matemáticas hasta el día de hoy.
Puntos clave sobre los aportes de René Descartes a las matemáticas
- Introducción de las coordenadas cartesianas.
- Desarrollo de la geometría analítica.
- Establecimiento de la relación entre álgebra y geometría.
- Influencia en el desarrollo del cálculo diferencial e integral.
- Publicación de «La Géométrie» como obra clave.
- Fomento de un enfoque lógico y sistemático en las matemáticas.
¡Te invitamos a dejar tus comentarios sobre este artículo! No olvides revisar otros artículos en nuestra web que también podrían interesarte.